• Date / Duration: 2021–2022
• Contributors: Jiashun Pang
• Status: Completed
• Affiliation: Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Acadymy of Sciences

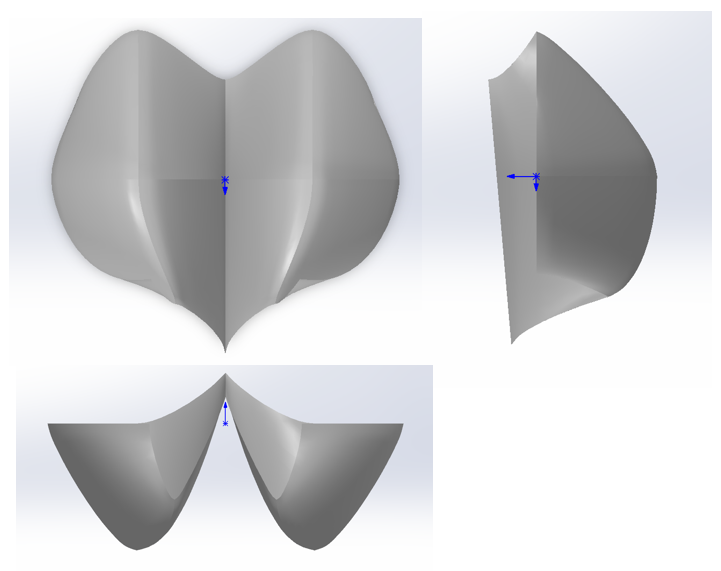
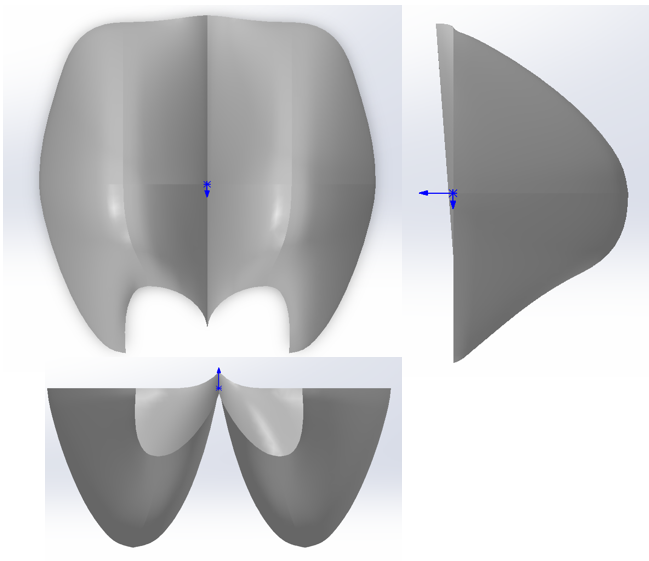
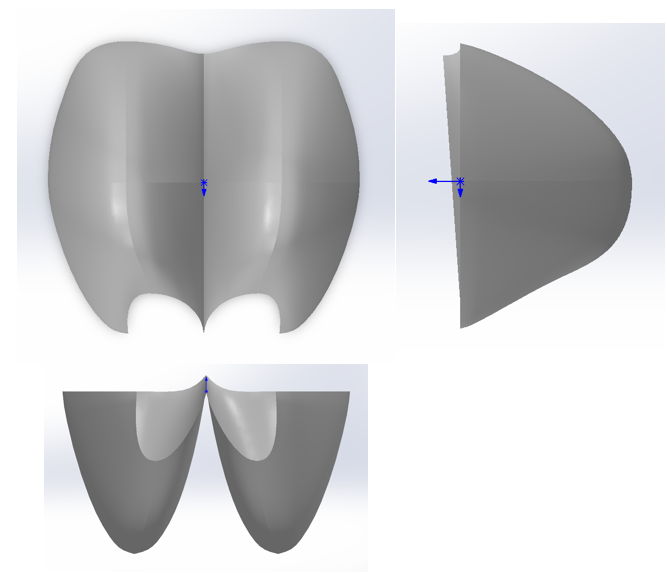
Project symmary

This project focused on the parametric design of Pelton turbine buckets using Bézier surfaces as a mathematical foundation. By leveraging Bernstein basis functions, bucket geometries were represented in a smooth, flexible, and rigorous manner. A MATLAB-based GUI was developed to support interactive parameter adjustment, visualization, and export, enabling users to explore a broad design space beyond conventional models.

The application evolved iteratively across three versions: from a simple prototype that generated Bézier surfaces, to a tool supporting symmetry operations, geometry thickening, and post-processing for CFD readiness. The final version provided both STL and STEP outputs, with adjustable tessellation resolution, bridging the gap between mathematical modeling, CAD interoperability, and CFD simulation workflows.

Although initially developed without prior programming experience outside MATLAB, this project marked a turning point in my research approach. It not only demonstrated the feasibility of automated geometry–simulation coupling, but also served as the seed of my long-term vision — the development of a “Machine Scientist” capable of unifying parametric modeling, CFD, and reasoning-driven optimization.

1. Motivation

This engineering project aims to develop a parametric modeling tool for designing a new Pelton turbine bucket, with design parameters extending far beyond existing models, in pursuit of higher efficiency and reliability. In this scenario, the lack of both historical datasets and experimental data makes traditional data-driven evaluation or benchmarking infeasible. Rather than keeping the geometry fixed and only tuning CFD conditions, our approach couples parametric geometry modeling with CFD simulations, enabling both domains to co-evolve through parameter variation. To this end, we are exploring an automated workflow that integrates the modeling stage with CFD into a feedback loop, iteratively refining the design until an optimized model emerges. This effort also represents the initial step toward my long-term vision — the development of a “Machine Scientist.”

2. Principle

2.1 Bernstein basis function

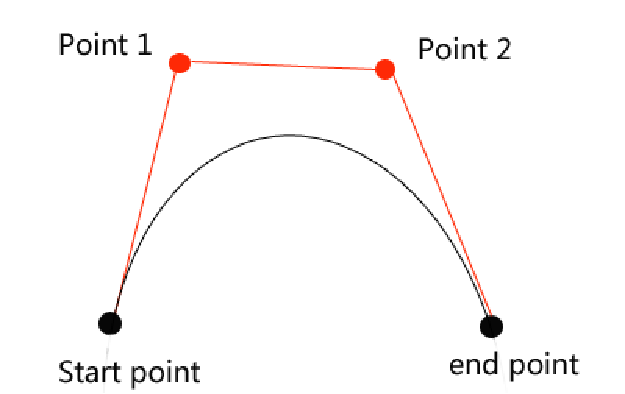
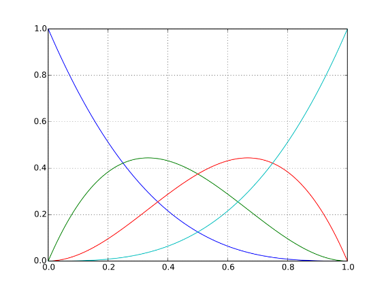
The construction of a Bézier curve is based on Bernstein basis functions, which determine how control points influence the final curve.
For a cubic Bézier curve, the parametric representation can be written as:

where $Q_u$ is a point on the curve at parameter $u \in [0,1]$, $p_i$ are the control points, and $B_i(u)$ are the Bernstein polynomials of degree 3.

Explicitly, the four basis functions are:

These functions have the following important properties:

• Non-negativity: $B_i(u) \geq 0$ for all $u \in [0,1]$.
• Partition of unity: $\sum_{i=0}^3 B_i(u) = 1$, ensuring the curve always lies within the convex hull of its control points.
• Local control: Each $B_i(u)$ determines the influence of control point $p_i$ along the curve, as illustrated in the right figure.

Together, these properties guarantee that Bézier curves are smooth, stable, and intuitive to design using control points, as shown in the left figure.

2.2 Bézier surface

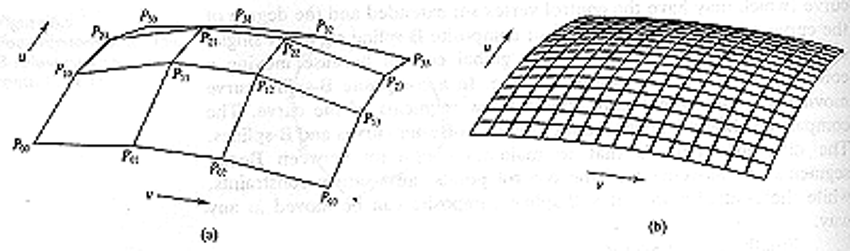
In this project, the bucket geometry is generated using bicubic Bézier surfaces, which provide a flexible yet mathematically rigorous representation of complex curves. The surface is defined by a grid of control points $p_{ij}$, with the shape interpolated through Bernstein basis functions $B_{i}(u)$ and $B_{j}(v)$:

Here, u and v are parametric coordinates, and the basis functions ensure smooth transitions across the surface. The figure above illustrates this construction process: starting from the control mesh, passing through a coarse polygonal form, and resulting in the final smooth bucket surface suitable for turbine flow simulations.

2.3 STEP and STL in Computer Graphics

In addition to the mathematical foundation of Bézier curves and surfaces, it is important to briefly introduce the output formats used in computer graphics and engineering applications. Two of the most widely used formats are STEP and STL, which serve different purposes in the design-to-simulation workflow.

• STL (Stereolithography format): Primarily used for 3D printing and CFD/FEA meshing, STL represents geometry as a collection of triangular facets. It provides a lightweight description of the surface, making it suitable for numerical simulations. However, STL does not store parametric or topological information, which can limit its accuracy in CAD editing.

• STEP (Standard for the Exchange of Product Data): A neutral CAD format standardized as ISO 10303, STEP preserves full parametric and topological information, including surfaces, edges, and assembly structures. It is widely adopted for data exchange between CAD systems and serves as a reliable format for subsequent modifications or integration into engineering workflows.

In practice, STL is typically used for downstream simulation tasks such as CFD, while STEP is preferred for geometric consistency and interoperability in CAD. In this project, both formats are supported to bridge the gap between surface modeling and engineering applications.

3 Application to bucket design

In this chapter, the Bézier surface formulation introduced earlier is applied to the practical design of a Pelton turbine bucket. The process is organized into three stages: the translation of Bézier surfaces into bucket geometry, the development of a MATLAB-based parametric GUI, and the post-processing of the generated models for further analysis and simulation.

3.1 From Bézier surfaces to bucket geometry

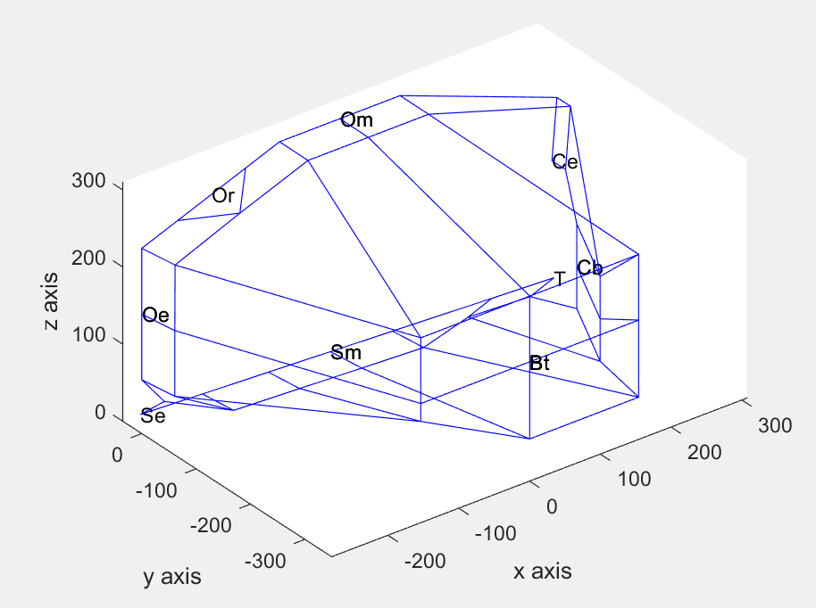
In this subsection, we apply the Bézier surface approach to the design of a Pelton turbine bucket. Specifically, we adopt the control-point layout reported by Vessaz et al. (2017) and embed it directly into our workflow. Rather than pursuing mathematical optimization, the literature-provided control points are used as the geometric foundation, allowing us to validate our parametric modeling tool and establish a consistent starting point for subsequent CFD coupling and performance analysis.

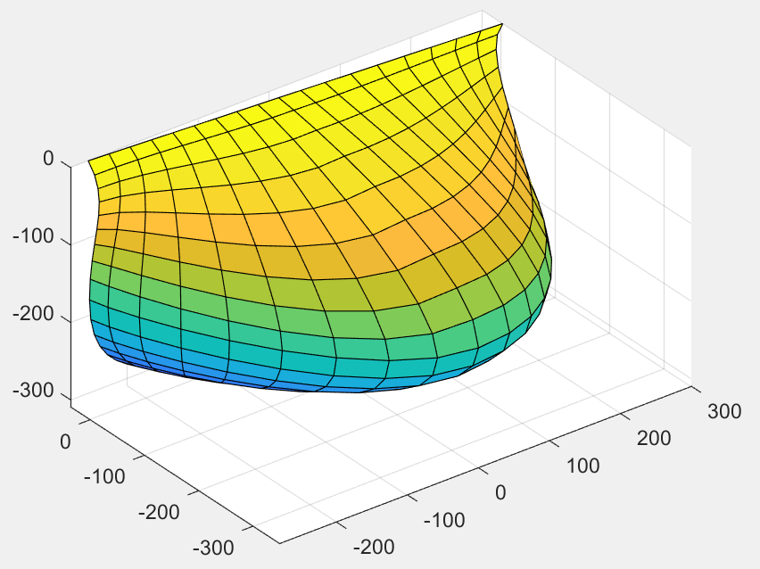
The construction process follows a clear sequence. First, a control-point framework is established to define the basic geometric skeleton of the bucket. Next, a Bézier surface is generated from these points, producing a smooth and mathematically consistent representation. To obtain the full bucket geometry, the framework is mirrored, ensuring symmetry across the bucket structure. Finally, the complete bucket surface is generated using the Bézier formulation, yielding a continuous and well-defined geometry suitable for engineering applications.

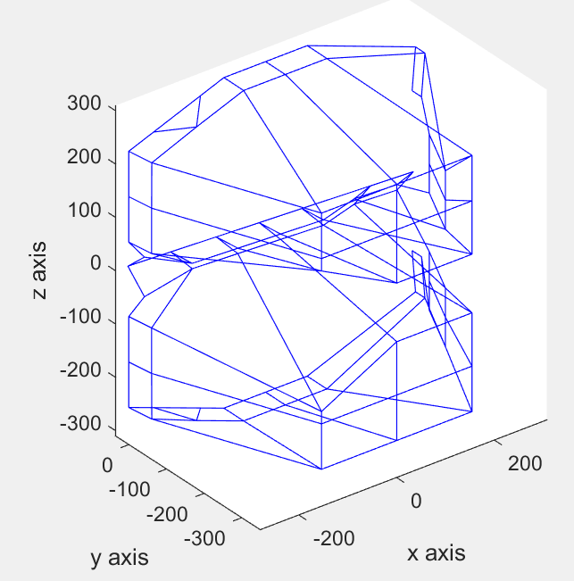
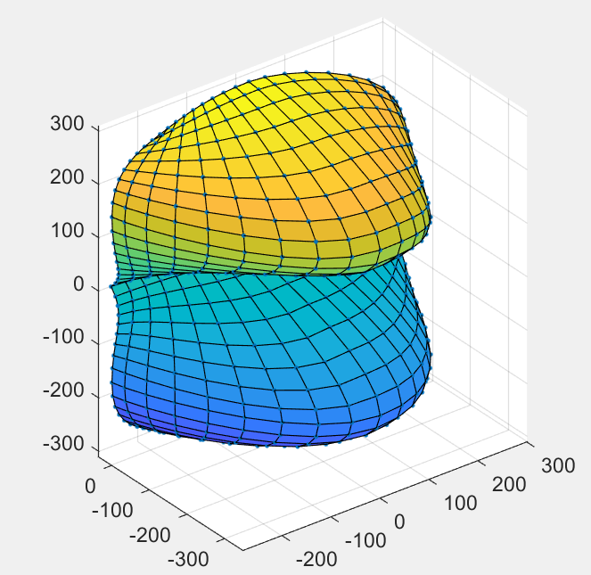
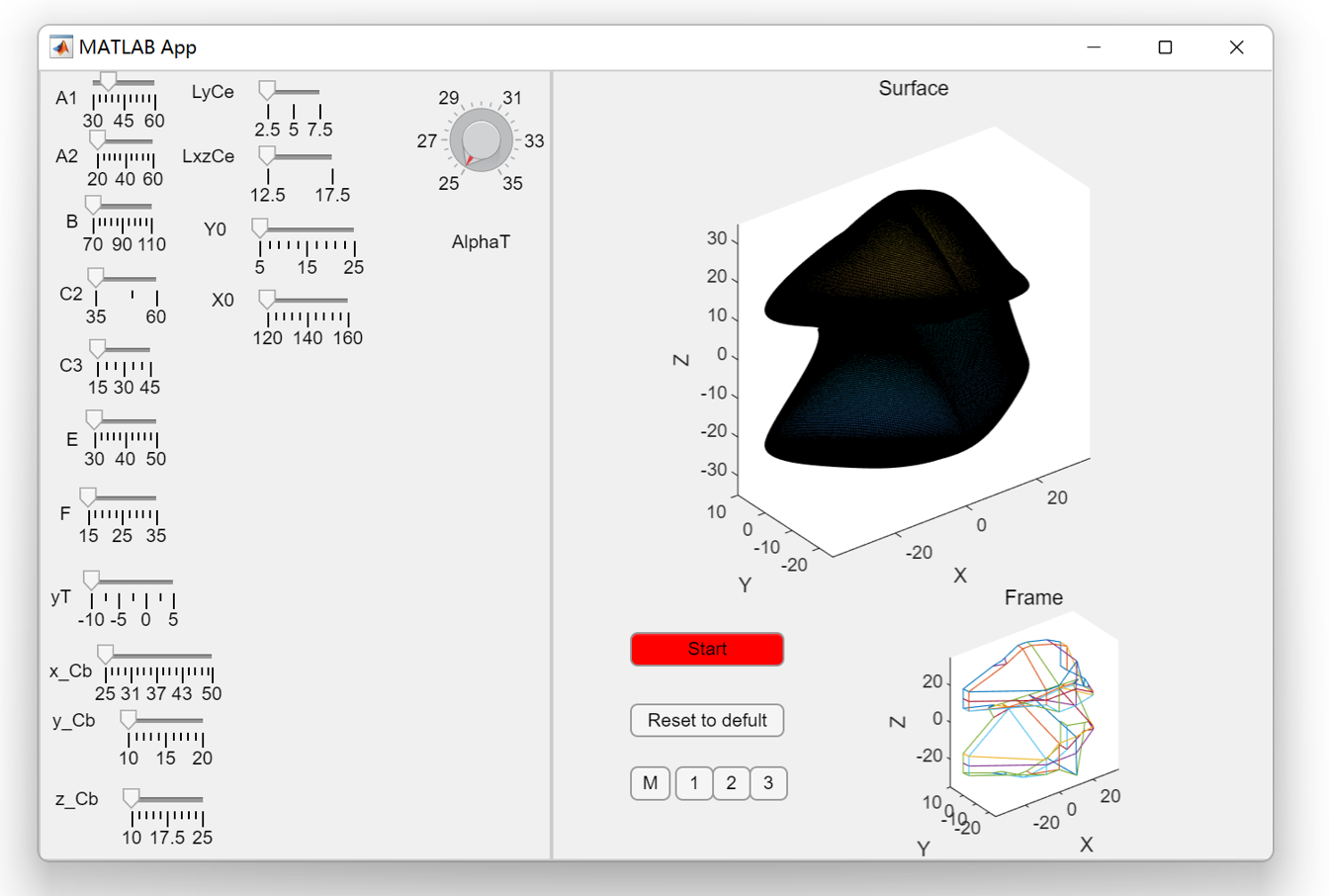
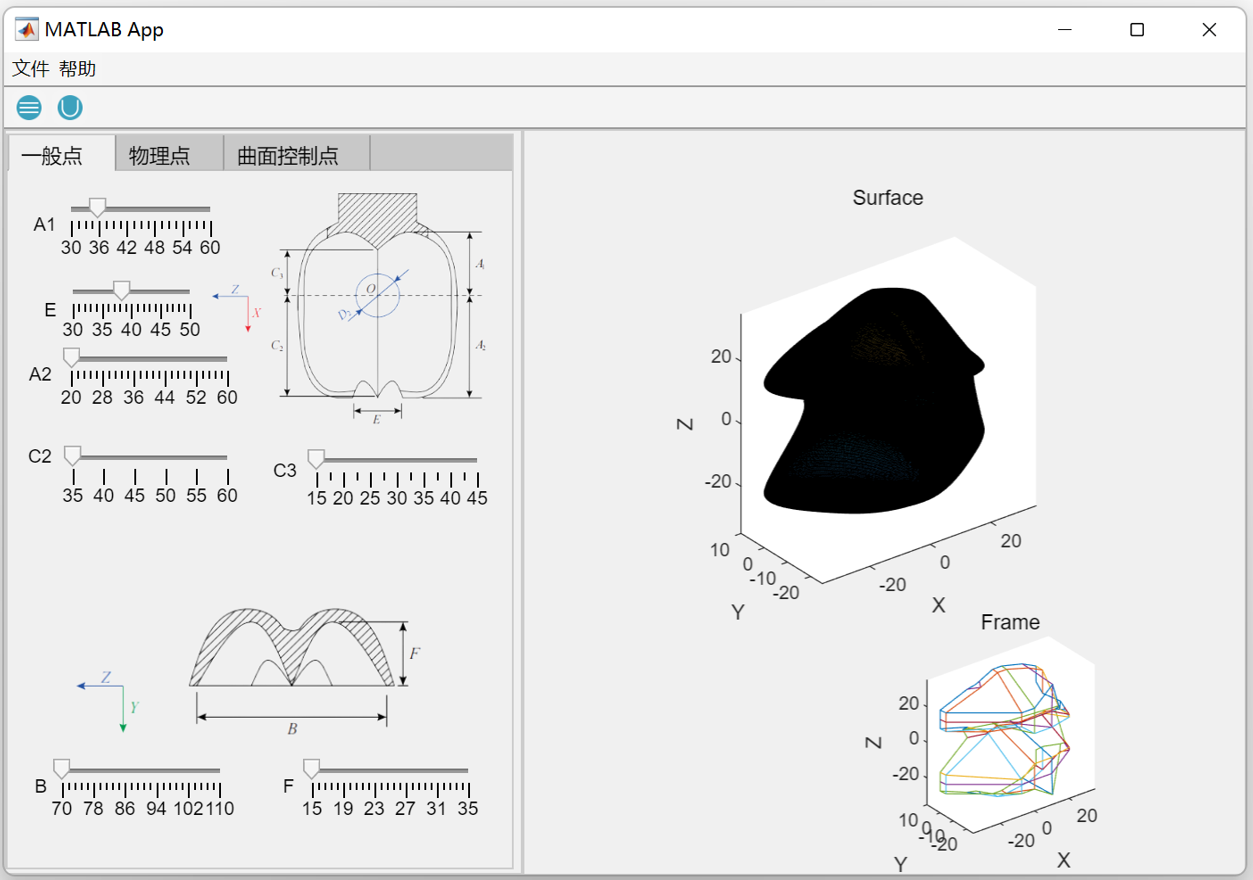
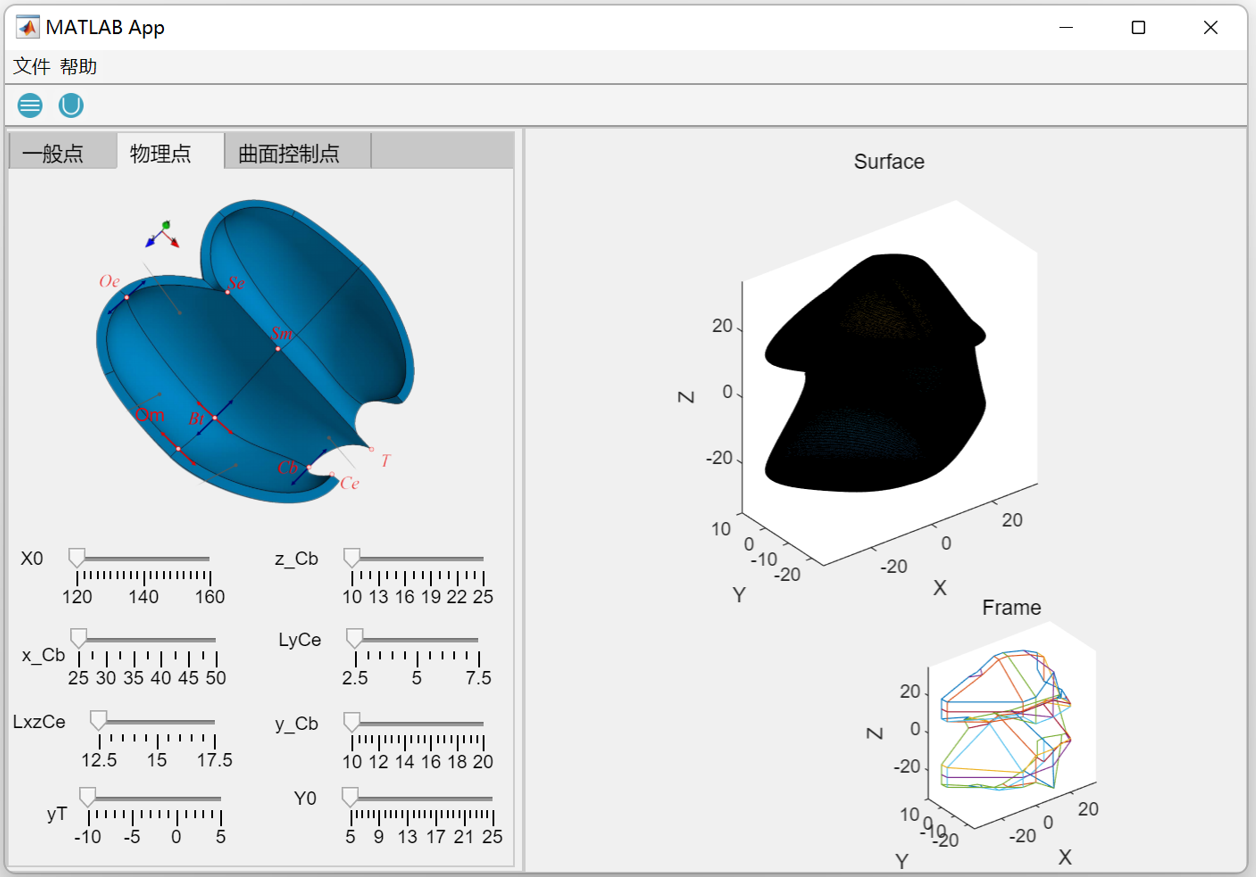
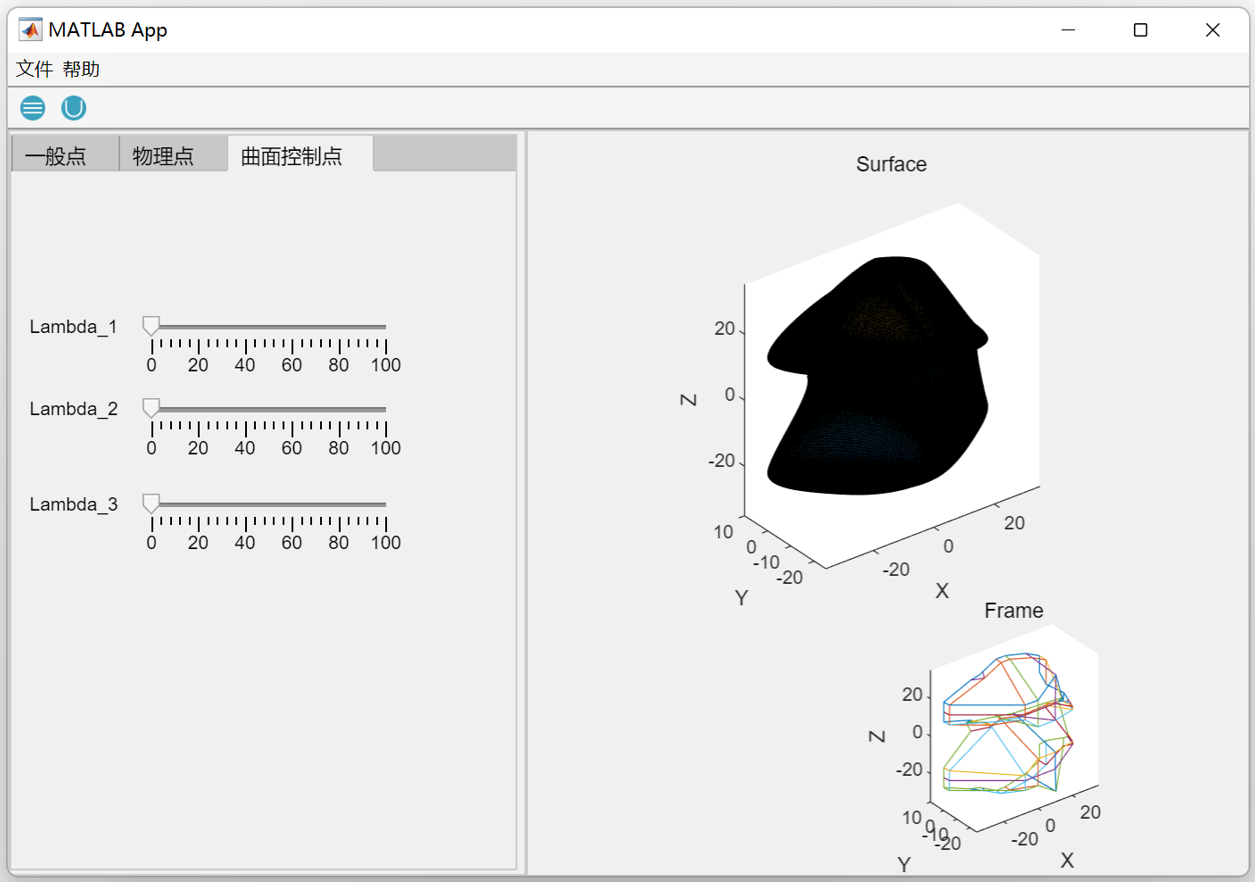
3.2 Development of the MATLAB GUI tool

To support a broad range of users, the GUI integrates several functional modules, including parameter input panels, real-time 3D visualization, and export options for downstream CFD analysis. Control points can be either manually defined or imported from external files, and sliders are provided to adjust geometric parameters interactively. The back-end routines automatically update the Bézier surface and regenerate the bucket geometry in response to user inputs, ensuring a smooth workflow from design exploration to model export. In addition, the GUI supports exporting the generated surfaces into standard CAD and CFD formats, bridging the gap between conceptual modeling and numerical simulation.

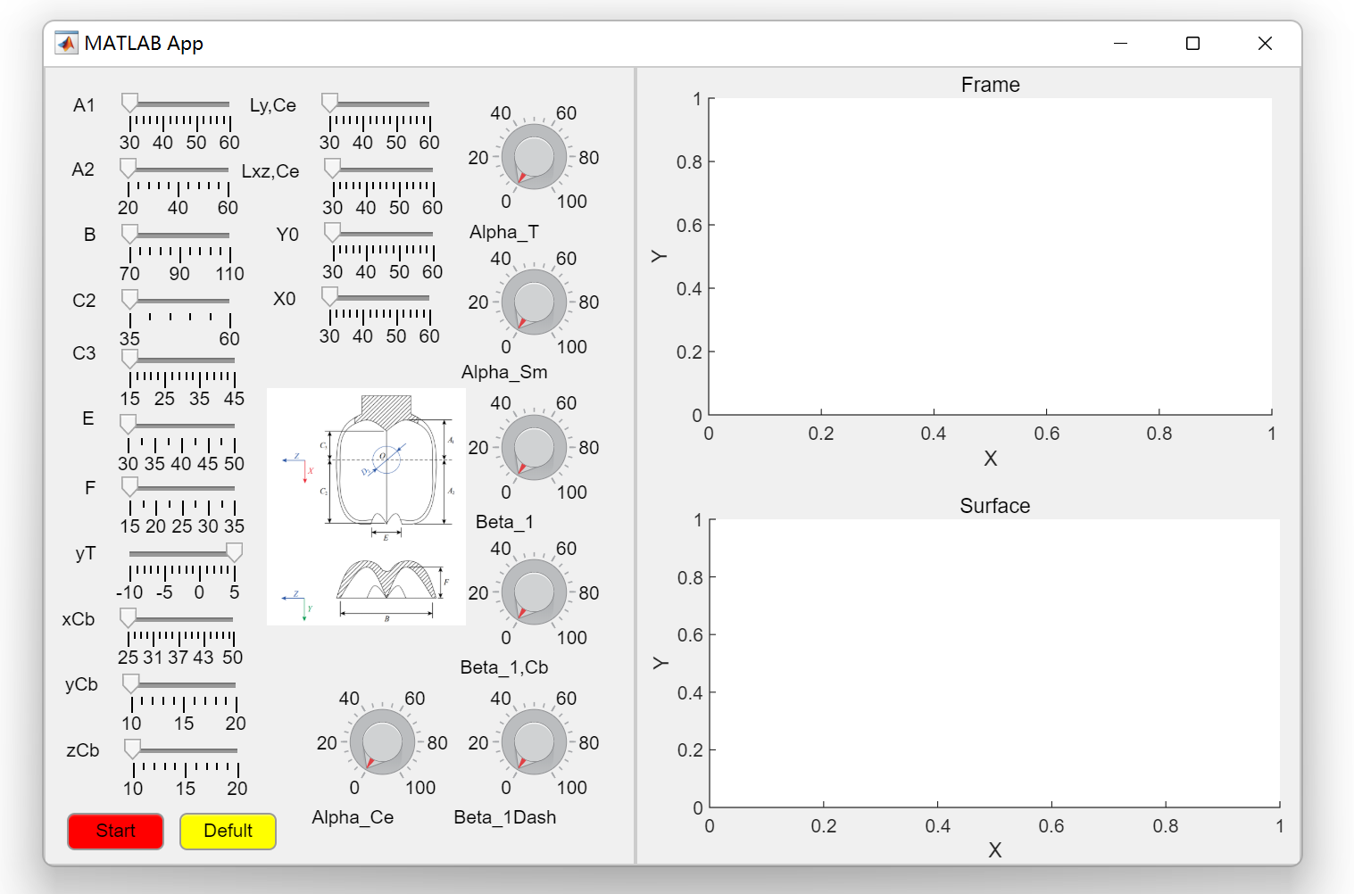
After the geometry is generated, two output strategies are implemented in the GUI to prepare the model for downstream use:

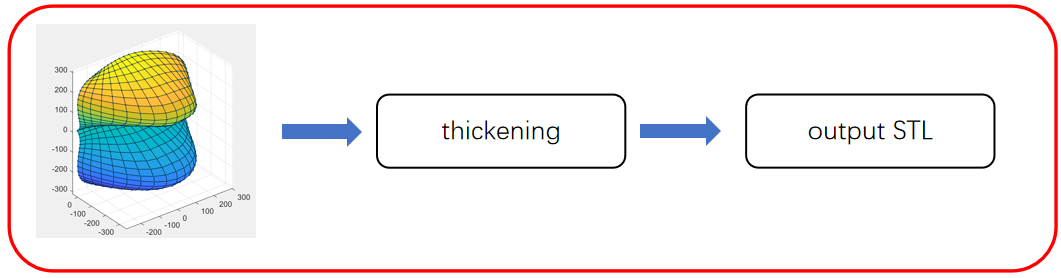
Patch-wise thickening: Each surface patch is thickened along its normal direction, followed by a fusion step to assemble the bucket as a solid body. This approach preserves local surface definitions but may introduce discontinuities at patch boundaries.

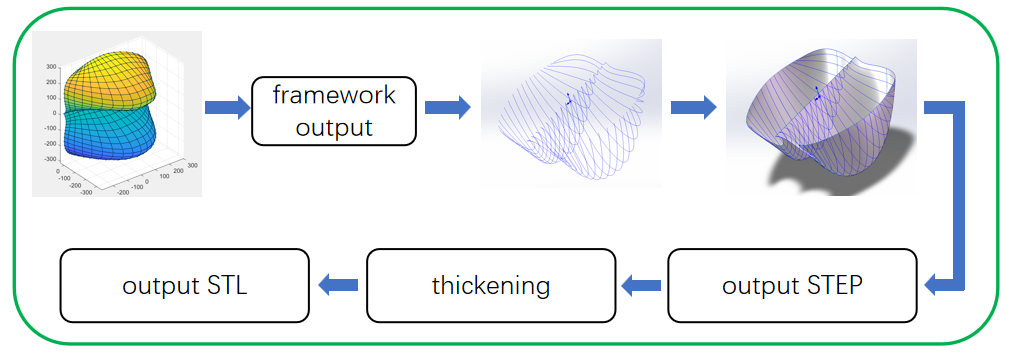
STEP-based thickening: Alternatively, all surface patches are first merged and exported as a single STEP file. A global thickening operation is then applied to the unified geometry (Figure 2). This strategy produces a consistent solid model and is generally more robust for CAD/CFD integration.

Both methods provide STL output for meshing and CFD simulations, while the STEP-based approach also enables compatibility with standard CAD workflows.

3.3 Geometry post-processing

After the bucket geometry is generated, post-processing is performed to prepare the model for analysis and simulation. This stage includes surface smoothing, mesh generation, and the export of geometry in formats compatible with CFD solvers.

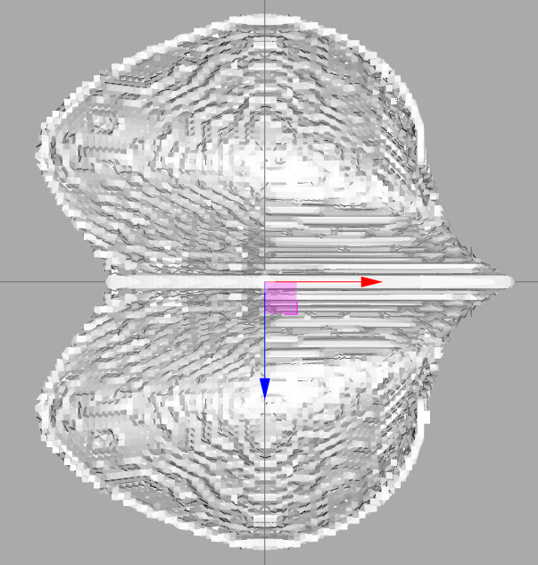
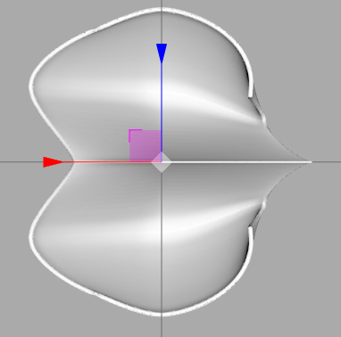
A key step in this stage is the adjustment of STL resolution, which directly controls the fidelity of the triangulated surface representation. By refining the tessellation (smaller facet size and lower chordal deviation), the exported STL more accurately captures the bucket geometry, leading to higher-quality CFD meshes and improved prediction of local flow features. However, increasing resolution also results in larger file sizes and higher computational cost. Conversely, coarser STL settings reduce the number of facets and accelerate meshing and simulation, but at the expense of geometric accuracy.

Therefore, the STL resolution is carefully tuned to achieve a balance between capturing sufficient geometric detail for hydraulic performance evaluation and maintaining feasible computational times for iterative CFD studies.

4. Iterative Development of the Application

The development of the parametric design application followed an iterative process, with three major versions being implemented and refined. Each iteration introduced new functionalities, improved usability, and addressed limitations identified in earlier stages.

• Version 1 – Prototype Interface
  The initial version focused on building a functional prototype in MATLAB GUI. It enabled basic parameter input, Bézier surface generation, and visualization of the bucket geometry. Although limited in functionality, this version served as a proof-of-concept and provided the foundation for subsequent improvements.

• Version 2 – Enhanced User Interaction
  In the second iteration, several improvements were introduced to make the design process more robust and user-friendly.
  1. A parameter linkage and constraint mechanism was implemented to reduce the number of free parameters and prevent unrealistic geometries, thereby improving model reliability.
  2. A wireframe visualization mode was added, enabling users to better inspect the control-point framework and geometric structure before generating the full surface.
  3. The GUI was extended to store up to three design configurations prior to export, allowing preliminary batch processing and reducing overall design time.

  Together, these enhancements made the workflow more intuitive, minimized errors, and enabled efficient exploration of multiple bucket design variants.

• Version 3 – Integration with Post-processing
  The final version further optimized the GUI and extended the workflow to include post-processing functionalities.
  1. GUI optimization with segmented output was introduced, making the interface more user-friendly and allowing users to manage outputs in a step-by-step manner.
  2. Export formats and strategies were refined, supporting both STL and STEP outputs. In addition, the triangulation resolution of STL files became adjustable, enabling users to balance CFD accuracy with computational cost.

  With these improvements, the application evolved into an end-to-end tool, covering the entire process from control-point definition to surface generation, thickening, and preparation for simulation.

Through these three iterations, the application evolved from a simple GUI prototype to a comprehensive design tool, capable of bridging the gap between mathematical surface modeling and practical CFD-based performance evaluation.

5. Conclusion and Reflections

In this project, we demonstrated how Bézier surfaces can be applied to the design of Pelton turbine buckets, starting from the mathematical foundation of Bernstein basis functions to the implementation of a MATLAB-based parametric GUI. The workflow was extended with post-processing strategies, enabling both STL and STEP exports, adjustable triangulation resolution, and geometry thickening for CFD simulations. Through three iterations of development, the application evolved from a simple prototype into an end-to-end tool that bridges surface modeling with engineering analysis.

Reflections.
At the time of starting this work, I had no experience with Python and relied entirely on MATLAB. While MATLAB provided a rapid prototyping environment, its closed ecosystem and the lack of command-line interaction became clear limitations for building extensible workflows. This realization motivated me to begin learning Python and to adopt it in my subsequent projects.

Moreover, this work represented the first attempt to conceptualize an automated workflow for parametric design and simulation. Although simple in scope, it laid the groundwork for the automation philosophy that later shaped the MosaicX project. In retrospect, the Pelton bucket tool was not only a practical application of Bézier surfaces but also the seed of the “Machine Scientist” vision, reinforcing the idea that scientific discovery can be supported by automated, reasoning-driven computational systems.

6. References

1. Vessaz, C., Andolfatto, L., Avellan, F., & Tournier, C. (2017). Toward design optimization of a Pelton turbine runner. Structural and Multidisciplinary Optimization, 55(1). https://doi.org/10.1007/s00158-016-1465-7